
BlockBase Token Distribution Roadmap
Ricardo Schiller - September 9, 2019
The development of BlockBase has been a very enriching experience for our team. Since its inception in 2017, we’ve gone through many important and special milestones.
Probably the most important one so far has been the attainment of financing from the EU through the Portugal 2020 program. This enabled us to build a solid and diversified team, that since the 8th of October 2018 has been working very hard on the creation of BlockBase.
We’ve already built most of the core functionalities of the platform, but for strategic reasons we haven’t disclosed yet our source code on github.
Now we’re entering an important stage where all our efforts and dedication during the past year will finally come to light.
BlockBase token allocation
BlockBase will have a total of 100,000,000 tokens. 45% of these tokens will be distributed during the first 2 years, as will be explained below. An additional 10% of the tokens will also be distributed during those 2 years, but to select strategic market makers. If any of these 55% of tokens to distribute still remain after the 2 years of distribution, they will either be burnt or distributed on a final airgrab with a uniform distribution. The remaining 45% of tokens, which are withheld from the token distribution, will be used to finance BlockBase operations such as product development and R&D, marketing and sales, ecosystem funding, partnerships, and acquisitions.
BlockBase token distribution
BlockBase is almost reaching its first anniversary, and in preparation for it we’ll start to disclose some of our code on github. On the day of the anniversary, we’ll start our token distribution. We’ve devised a detailed plan for our token distribution that relies on the concept of the airgrab, but that distinguishes itself from other airgrabs that have been performed on EOS.
After analyzing many other airgrabs, we’ve identified two important flaws in the way they are designed and executed:
-
Each airgrab has a short duration, which usually leads to the distribution of tokens amongst a small number of participants. Those get all the tokens, resulting in a very narrow token distribution.
-
The amount of tokens distributed per participant is usually proportional to the number of EOS each owns. This means that even if the distribution of tokens is broad, those who hold small amounts of EOS will be enormously disfavored in comparison to those who hold large amounts. This discourages participation of those who own few EOS, which further narrows the distribution.
In our opinion, airgrabs can and should be improved. The goal of an airgrab is to distribute the tokens as broadly as possible. Its success may be directly measured by this metric, where a poorly executed airgrab may compromise the future success of the project as a whole.
With this in mind, we’ve developed a new type of airgrab that differs from all other typical airgrabs in the following ways:
-
Instead of having only one airgrab, we’ll have monthly airgrabs during 2 years, resulting in 24 airgrabs in total. Each airgrab will distribute one seventh of the remaining tokens to distribute.
-
In each airgrab, the quantity of tokens distributed per participant will be much more uniform than usual. This distribution is calculated through a mathematical function we’ve designed for that purpose, which is detailed further ahead.
There are several reasons to design our airgrab model as such. We are striving for a just and broad distribution of tokens.
A token distribution with 24 monthly airgrabs
It takes a reasonable amount of time for the masses to get to know the potential of a given project. Sometimes it takes years for the awareness to spread. If an airgrab’s duration is too short, there won’t be enough time for most potential users to get to know the project nor for them to determine its value. This can be solved through a gradual distribution of tokens, but early adopters should be favored nonetheless. Accordingly, it makes sense to perform several consecutive airgrabs, where the quantity of coins is gradually reduced.
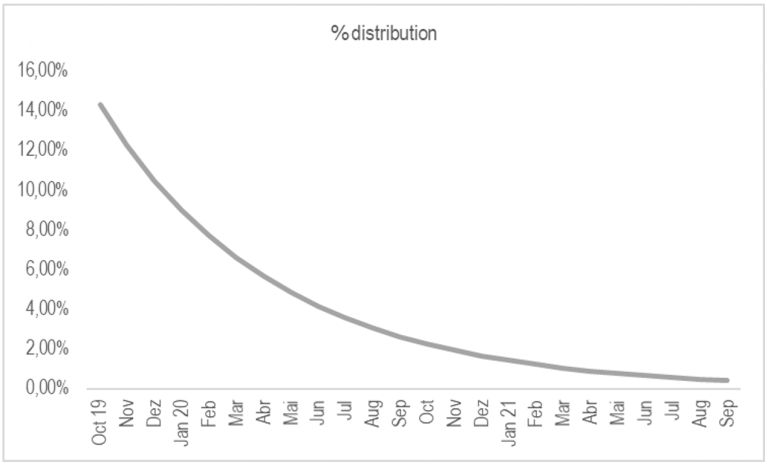
It isn’t easy to choose the right number of airgrabs and fractions of tokens to distribute. In our case, we believe it makes sense to have 24 airgrabs, where each one distributes one seventh of the remaining tokens to distribute. This distribution is plotted in figure 1.
This approach leads to a distribution with interesting characteristics. On the first month, 14.29% of the tokens will be distributed. In comparison to a uniform token distribution during 24 months, which would result in a monthly token distribution of 4.17%, we are distributing 3.4 times more than the corresponding value in the uniform distribution.
This clearly favors the early adopters that participate in the first airgrab. But it doesn’t favor them inordinately. At the end of the first year we’ll have distributed almost 85% of the tokens, with only 15% left to distribute during the second year.
This will result in ample time to participate in the first airgrabs, but without preventing the participation of latecomers.
Why the conventional way of distributing tokens should be improved
The goal of an airgrab is to distribute the tokens as broadly as possible. The airgrab concept came from a change of its ancestor, the airdrop, which wasn’t easy to execute because it required a costly reserve of RAM. Both the airgrab and the airdrop use, by convention, the quantity of EOS each participant holds as a reference to figure out the quantity of tokens each participant will receive. This leads to a distribution that favors those who have a lot of EOS, and neglects those who have little. Furthermore, it may narrow the token distribution because those who have little EOS and which constitute the majority of potential participants know that they won’t benefit that much in participating in the first place.
A quick analysis of the data shown on https://bloks.io/topholders, shows us that currently 74% of all EOS is stored in just 100 accounts (analyzed at 05/09/2019). This is an extremely centralized distribution of tokens.
An alternative way to the conventional distribution of tokens is to perform a uniform token distribution. In this approach, all receive the same amount of tokens. The advantage of this approach is that the majority of participants will receive much more than in a distribution that is proportional to the participants’ EOS holdings, because the enormous quantity of tokens that large EOS holders would receive is distributed amongst all participants. Additionally, this approach promotes a higher participation than the conventional distribution approach, because the vast majority has a much higher motivation to participate.
But we want to go a step further from the uniform token distribution. Although being a much fairer distribution than the distribution in function of EOS holdings, a uniform distribution may lead to weaker market dynamics. To solve this, the distribution will be slightly skewed, where some will receive more and others will receive less. The interesting part of it is that the choice of who receives more and who receives less is done by a random process. This resembles a lottery, but where all win, just that some win more and others win less.
This approach makes sense for two main reasons. The first reason is to avoid a distribution that is completely uniform. The second reason is to promote even more the participation in the token distribution. The participants may receive even more tokens than in a uniform distribution.
BlockBase token distribution model per airgrab
Before we step into the details of the equation that determines how the token distribution is done, let’s see how it looks on a chart in comparison to a uniform distribution. Figure 2 shows a scenario of 100 participants, to whom we distribute 100 tokens. In the case of a uniform distribution, all participants would receive 1 token. Using our distribution model, the luckiest participant will receive about 4.17 tokens and the unluckiest participant will receive about 0.38 tokens. The luckiest participant will receive about 11 times more than the unluckiest one. Although the distribution isn’t uniform, the quantity of distributed tokens gets very close to the same 100 tokens, because…math.
This equation can be applied to any number of participants and to any number of tokens. The resulting distribution will produce a curve with similar characteristics.
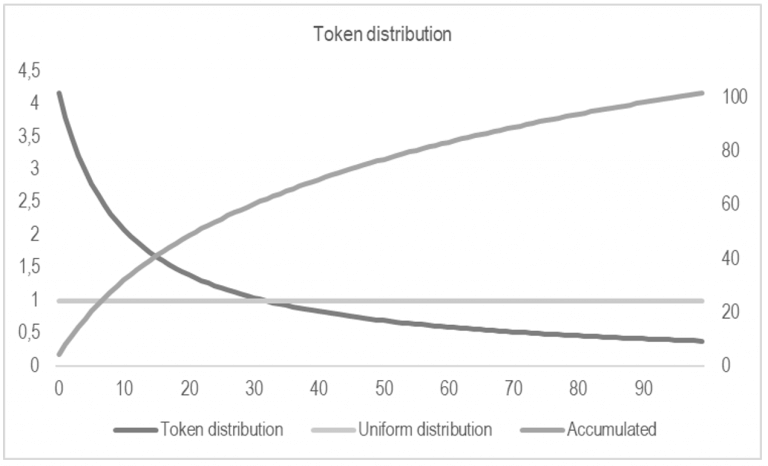
Figure 2 – Comparison between a uniform distribution of tokens and the distribution we’ll use
The equation that we use to calculate the distribution, and that produces the curve shown on figure 2, is the following:
This equation seems complex but it is rather simple. This equation can be represented by three parts:
-
– Corresponds to the number of tokens each participant would receive in a uniform distribution.
-
– Corresponds to an equation that models a horizontal asymptote to 0 that crosses y at 1.
-
– Corresponds to a constant that raises B by a specific amount necessary to assure that a similar quantity of tokens to T are distributed, although dealing with an asymptote function.
Figure 3 presents with simplicity the way the function works. If we used only the equation that models the asymptote, defined by f(x) = A x B, the total amount of distributed tokens would be much less than with a uniform token distribution.
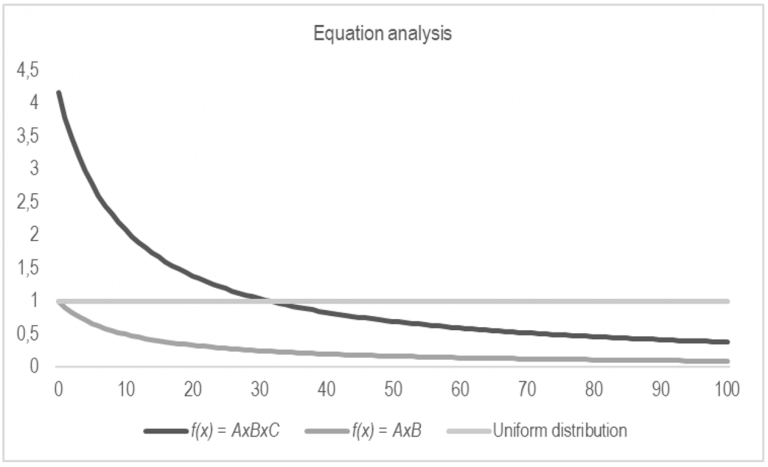
Figure 3 – Comparison between equation f(x) = A x B and f(x) = A x B x C. It’s clear that, in order to distribute a similar amount of tokens to a uniform token distribution, it’s necessary to raise the equation by a specific quantity. This quantity is defined by C
To compensate this deviation, it’s necessary to multiply the equation by C, which is calculated through  , whose details we leave out of this article. Even though using an integral to calculate C isn’t exactly the right approach to solve this problem due to the function being discrete and not continuous, its calculation is easy and produces very satisfactory results, and is easy to explain and understand.
, whose details we leave out of this article. Even though using an integral to calculate C isn’t exactly the right approach to solve this problem due to the function being discrete and not continuous, its calculation is easy and produces very satisfactory results, and is easy to explain and understand.
Published by Ricardo Schiller
Lead Architect